土地の境界・筆界アドバイス
土地の境界・筆界
アドバイス
2023年11月号
土地の境界がわからない、調べてもはっきりしない。現地でも、机の上でも、わかりづらい土地の境界について、具体例を交えて、できる限りわかりやすく伝える（ことを目的とした）、土地家屋調査士が解説したアドバイスです。
求積法によって土地の面積は変わる？
登記所には、土地の地積、辺長、形状などを明らかにする「地積測量図」という図面があります。
これは、一筆の土地の地積に関する測量の結果を明らかにする図面で、登記の申請時に提供されたものです。
地積測量図が法定添付書類（法令によって添付が定められた書類）となったのは昭和35年4月からですので、それ以降に「土地表題登記」「土地地積更正（又は変更）登記」「土地分筆登記」のいずれかが申請された土地については、地積測量図が備え付けられていることになります。
さて、「測量の結果を明らかにする図面」とはいいますが、この「測量」については色々な精度があります。
つまり、「測量した結果だから土地の地積は正しい」とはいえないものも多々あるのです。
今回は、地積測量図における求積法の違いについてお話をしたいと思います。
昔ながらの求積法である「三斜法」
過去と今では、測量の精度は大きく違います。
それこそ地積測量図の提供が必要とされた昭和35年当時は、平板測量といって、平らな板の上にはりつけた図紙に、所定の縮尺の目盛を目で読み取って手書きでプロット・線引きしていくというものでした。
数百分の1という目盛ですから、1目盛違っただけでも数十センチの誤差が生じるわけです。
大まかな土地の形状は分かりますが、決して精度の良いものとはいえません。
（しかも、単位は現在と異なり尺貫法です）
そして、この頃の面積の計算方法は、三斜法と呼ばれるものでした。
三斜法とは、土地の筆界点同士を結んで複数の三角形を作り、それぞれの三角形の面積を求めて合計する、という方法です。
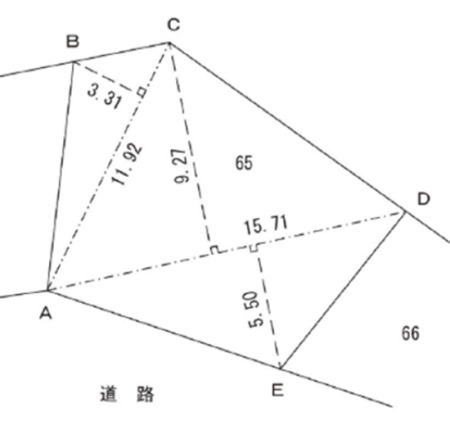
例えば、上記のようにABCDEで囲まれる一筆の土地を、３つの三角形で分割するわけです（一点鎖線が三角形で分割する線で、点線がその三角形の高さを表します）。
11.92×3.31÷2＝19.7276
15.71×9.27÷2＝72.81585
15.71×5.50÷2＝43.2025
合計 135.74595
このように、それぞれの三角形の面積を求め、これを合計することによって、最終的なABCDEで囲まれた範囲の面積を出すことができるのです。
ただし、各三角形の高さ（点線部分）は実際に測っているわけではなく、分割した後に図上で長さを読み取るので、決して精度はよくありません。
細かくチェックしてみると、数学的にみておかしな値が記載されていることがあります。
そのため、これで求められた面積も、信頼性が高いわけではないのです。
やがて測量機器が発達することにより、土地の形状は平板測量よりも正確に図示できるようになりましたが、求積法は依然として三斜法が使われていました。
高さの読み取り誤差も小さくはなりましたが、それでも誤差が生じることに変わりはありません。
結局、三斜法は、昭和後期まで主流となっていたので、今でもたくさん登記所に備え付けられています。
（ちなみに現在でも使われることがあります）
「座標法」への転換
その後、求積の主流は「座標法」へと変わります。
きっかけは昭和52年に、筆界点を復元可能なものとするよう取り扱いが変わったからです。
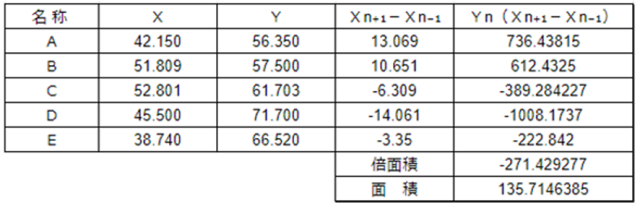
座標法とは、土地の筆界点を平面上の座標値として表し、その座標値によって面積を求めるものです。
上記のABCDEを測量による座標値で表し、座標法によって面積を求めると、例えば以下のようになります。
右下に表示されている数値が、座標法によって求めた面積です。
三斜法の面積と比較すると、若干異なっていることがお分かりでしょうか。
もちろん、こちらの方が正確です。
三斜法で行っている計算は「算数」レベルですが、座標法は「数学」レベルなのです。
このように、同じ土地の面積を計算しても、求積法が変わると値が変わります。
この土地の所有者さんは、「面積が少なくなった！」と思われるかもしれませんが、土地自体は変わっておらず、変わったのは求積方法なのです。
一般の方が求積法について知る機会はあまりないかもしれませんが、このコラムが一つのキッカケになれば幸いです。